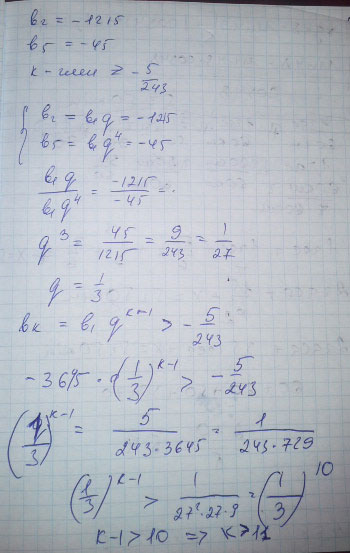Задача Найдите четвертый член ге ... равна 20, b1=22, (|q|<1) (на геометрическую прогрессию)
Арифметической прогрессией a n называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом d d — разность прогрессий. Геометрической прогрессией b n называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и тоже число q q — знаменатель прогрессии. Найдите двадцать второй член прогрессии. Найдите семьдесят пятый член этой прогрессии. Для арифметической прогрессии характеристическое свойство имеет вид.



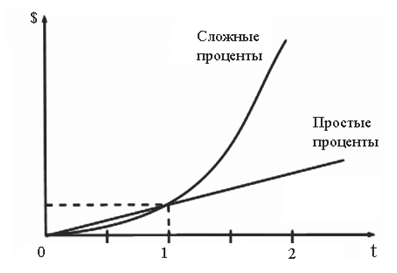



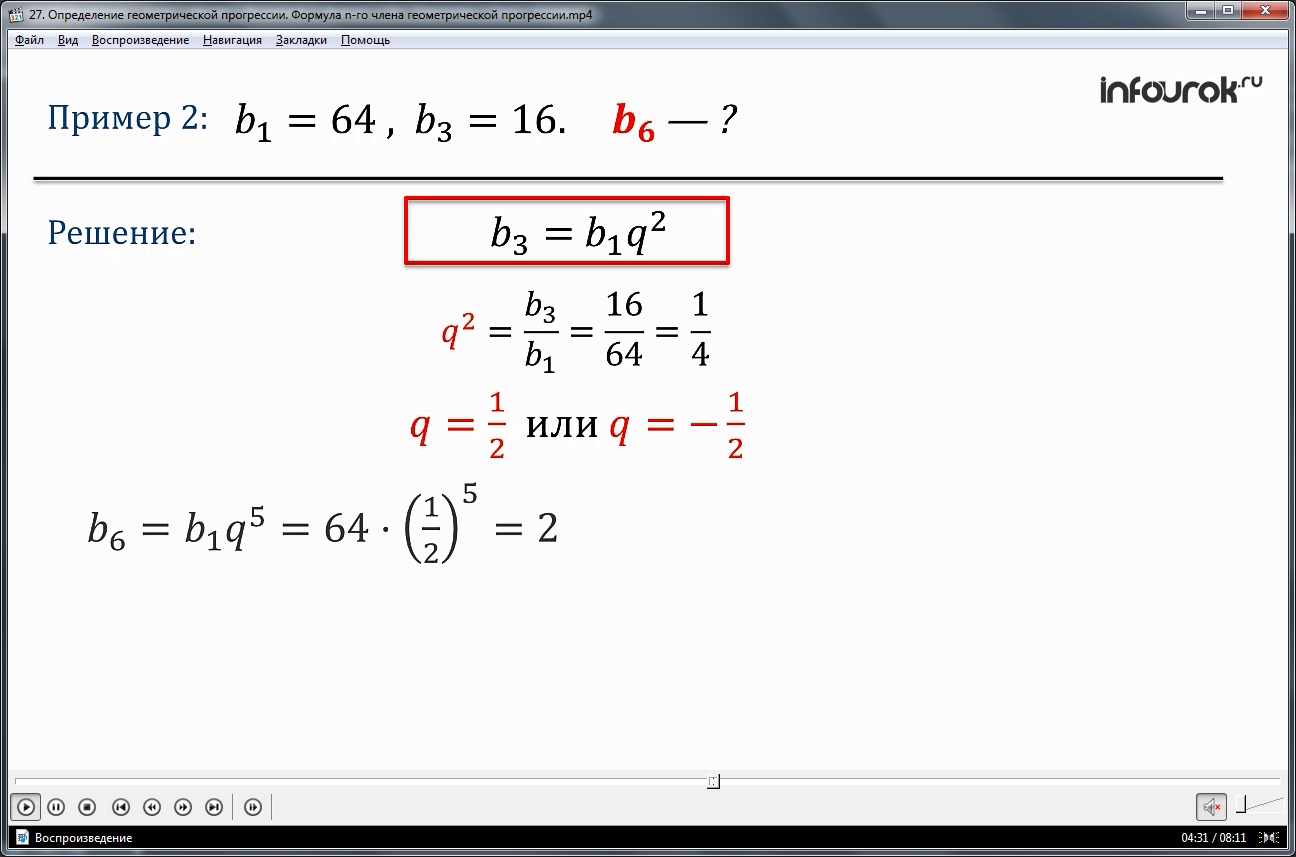


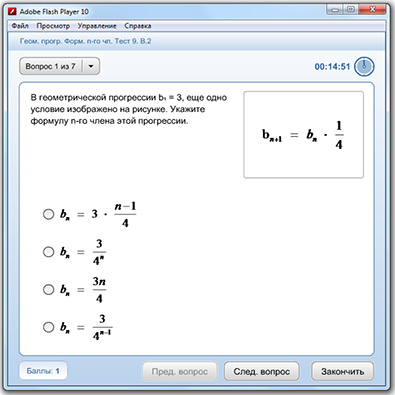
Это число называют знаменателем геометрической прогрессии. О том, откуда она взялась, где применяется, какими обладает свойствами, какие задачи помогает решать. Как обычно базовая глава — самая важная, потому что нужно не просто применять формулы, а понимать, что ты делаешь и зачем ты это делаешь. Если ты уже читал тему «Арифметическая прогрессия» ты можешь смело пропускать этот блок и переходить к самой сути. Если нет, то советую ознакомиться, чтобы иметь общее представление о том, что такое прогрессия в целом и с чем ее едят.

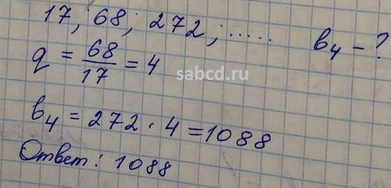





| 307 | Запиши число в поле ответа. Информация для покупателей. | |
| 55 | Давай рассмотрим последовательность, членами которой являются степени числа 2 с натуральными показателями:. Каждый член этой последовательности, начиная со второго, получается умножением предыдущего члена на 2. | |
| 305 | Геометрическая прогрессия. Формула общего члена геометрической прогрессии. | |
| 206 | Найдите первый член геометрической прогрессии. Информация для покупателей. | |
| 125 | В этом материале расскажем самое главное об арифметической прогрессии. Числовая последовательность — это множество чисел, каждому из которых можно присвоить уникальный номер. | |
| 376 | Точнее, от вашего браузера их поступает слишком много, и сервер VK забил тревогу. | |
| 149 | Сумма членов геометрической прогрессии. | |
| 163 | Рассмотрим последовательность, членами которой являются степени числа два с натуральными показателями: два, два квадрат, два куб, два четвертой степени и так далее. Каждый член этой последовательности, начиная со второго, получается умножением предыдущего члена на два. | |
| 330 | В любом учебнике по алгебре можно встретить огромное количество задач по геометрической прогрессии. Вместе с экспертом разбираемся, что это такое и как их решать. | |
| 476 | Пожалуйста, укажите электронный адрес или номер телефона, который вы использовали при регистрации. |
Господин Экзамен. Как пользоваться? Решение для на геометрическую прогрессию : Дана геометрическая прогрессия : 4, Найдите четвертый член геометрической прогрессии.